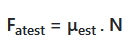Leis da fisica de Isaac Newton
"As leis de Newton fundamentam a base da Mecânica Clássica. São um conjunto de três leis capazes de explicar a dinâmica que envolve o movimento dos corpos. Essas leis foram publicadas pela primeira vez pelo físico inglês Isaac Newton, no ano de 1687, em sua obra de três volumes intitulada Princípios Matemáticos da Filosofia Natural.
A introdução das leisde Newton
"Um dos principais legados deixados por Isaac Newton foi a precisa explicação matemática para o movimento dos corpos. A Mecânica Newtoniana mostrou-se capaz de predizer a trajetória de asteroides e o surgimento das marés, tornando-se um dos marcos da Física por trazer equações matemáticas para a explicação de fenômenos naturais.
"Newton, após chegar à expressão da força gravitacional,
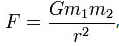 , a usou para realizar estudos e interpretar uma variedade de fenômenos que ocorrem na natureza como, por exemplo, as marés. Muitos dos fenômenos que ele estudou já eram conhecidos, só não havia uma explicação científica para eles. O sucesso que Newton obteve na explicação desses fenômenos constituiu um grande triunfo para a teoria da Gravitação Universal.
, a usou para realizar estudos e interpretar uma variedade de fenômenos que ocorrem na natureza como, por exemplo, as marés. Muitos dos fenômenos que ele estudou já eram conhecidos, só não havia uma explicação científica para eles. O sucesso que Newton obteve na explicação desses fenômenos constituiu um grande triunfo para a teoria da Gravitação Universal."A maré é um dos fenômenos naturais mais conhecidos. Esse fenômeno ocorre em razão do movimento periódico de subida e descida do nível da água, produzindo dessa maneira as chamadas marés altas e marés baixas. Foi Isaac Newton que, a partir da expressão da força gravitacional, deu a explicação para esse fenômeno natural. Segundo as explicações do físico e matemático Newton, as marés são causadas pela atração do Sol e da Lua sobre as águas do mar.
As Forças que atuam sobre as marés ocorrem porque a Terra é um corpo extenso e o campo gravitacional que é produzido pelo Sol ou pela Lua não é homogêneo em todos os pontos, pois tem alguns pontos da Terra que estão mais próximos e outros mais distantes destes corpos celestes. Esses campos gravitacionais provocam acelerações que atuam na superfície terrestre com diferentes intensidades. Dessa forma, as massas de água que estão mais próximas da Lua ou do Sol sofrem aceleração com intensidades maiores que as massas de água que estão mais afastadas desses astros. É essa diferença de pontos mais próximos e mais afastados do Sol e da Lua que dão origem às marés.
“Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças aplicadas sobre ele.”
Essa lei diz que, ao menos que haja alguma força resultante não nula sobre um corpo, esse deverá manter-se em repouso ou se mover ao longo de uma linha reta com velocidade constante. A Lei de Inércia também explica o surgimento das forças inerciais, isto é, as forças que surgem quando os corpos estão sujeitos a alguma força capaz de produzir neles uma aceleração. Por exemplo: ao pisar no acelerador do carro, um motorista pode sentir-se comprimido em seu banco, como se houvesse uma força puxando-o para trás. Na verdade, o que ele sente é a expressão de sua inércia, ou seja, a tendência que seu corpo tem de permanecer parado ou em velocidade constante.
A Primeira Lei de Newton é pouco intuitiva: ao rolarmos uma bola no chão, ela para diante de nossos olhos. Jamais esperaríamos que ela rolasse eternamente. No caso descrito, porém, a bola está sujeita a uma força resultante que não é nula: há uma força de atrito entre a bola e a superfície do chão, desacelerando o objeto continuamente.
A força de atrito surge em sentido contrário ao movimento de um objeto. Ela pode ser estática, se o objeto está em repouso, ou dinâmica, se o objeto está em movimento.
"Quando empurramos ou puxamos um determinado objeto tentando movê-lo, percebemos que existe certa dificuldade para colocá-lo em movimento. Essa dificuldade deve-se à força de atrito, que é uma força que se opõe ao movimento de objetos que estão sob a ação de uma força. Ela age paralelamente à superfície de contato e em sentido contrário à força aplicada sobre um corpo.
"A força de atrito deve-se à existência de rugosidades na superfície de contato do objeto com o solo. Essas rugosidades não são observadas macroscopicamente, mas são elas que dificultam o movimento. Observe na figura abaixo as irregularidades que existem no contato entre o bloco e a superfície:
Do tipo dos materiais que estão em contato: cada material tem suas características próprias. Quanto mais “lisos” ou “polidos” estiverem os objetos em contato, menor será a força de atrito. Essa propriedade é definida numericamente pelo coeficiente de atrito, que pode ser dinâmico ou estático, possuindo um valor diferente para cada material.
Força normal: trata-se da reação normal à superfície sobre a qual o corpo está apoiado e depende do peso do objeto. Quanto maior for a força normal, maior será a força de atrito.
Imagine que o bloco da figura acima esteja em repouso, mas deseja-se colocá-lo em movimento. Inicialmente se aplica uma força F, porém, ele continua em repouso, pois a força de atrito aumentará conforme se aumenta a intensidade da força F. Enquanto o bloco, mesmo sob a ação dessa força, continua em repouso, a força de atrito é denominada estática. Existe um determinado valor de F em que o bloco fica na iminência de movimento. Nesse ponto, a força de atrito é máxima e recebe o nome de força de atrito estático máxima. O movimento somente iniciará quando a força F for superior a essa força. A força de atrito estático é calculada com a equação:
"Sendo:
Fatd é a força de atrito dinâmico;
μd é o coeficiente de atrito dinâmico;
N é a Força Normal.
Os coeficientes de atrito estático e dinâmico são grandezas adimensionais, ou seja, não possuem unidade de medida e são representadas apenas pelo seu valor numérico.
Também é importante observar que o atrito dinâmico sempre será menor do que o atrito estático máximo. Isso se deve ao fato de que o coeficiente de atrito estático é maior que o coeficiente de atrito dinâmico:
"A importância da força de atrito
O atrito, muitas vezes, é visto como algo negativo. Que ver alguns exemplos? O atrito provoca desgaste em peças de máquinas, em solas de sapato; para vencer, o atrito os automóveis gastam mais combustível, entre outros. Porém, sem o atrito, seria impossível realizar algumas atividades essenciais, como andar ou colocar um automóvel em movimento. Entenda a razão:
Uma pessoa, ao caminhar, empurra o chão para trás com os seus pés. Isso faz com que surja uma força atrito em sentido contrário, ou seja, o chão passa a exercer uma força sobre a pessoa, empurrando-a para frente. Se não houvesse o atrito, ocorreria algo de forma semelhante a quando se tenta andar sobre um chão muito bem encerado ou com sabão. As pessoas escorregariam e jamais conseguiriam andar.
Quanto as rodas de um automóvel começam a girar, passa a existir um atrito entre elas e o chão que as impulsiona para frente. Se não houvesse o atrito, as rodas girariam, mas o carro não se movimentaria.
"Introdução sobre o movimento uniformemente variado
"Movimento uniformemente variado (MUV) trata-se de um movimento no qual a mudança de velocidade, chamada de aceleração, ocorre a uma taxa constante. O movimento uniformemente variado é um caso particular do movimento variado. Neste, a velocidade apenas varia, enquanto naquele a velocidade varia de maneira constante, isto é, sua magnitude sofre acréscimos ou reduções iguais, a cada segundo.
Quando algum móvel desenvolve um movimento uniformemente variado, a sua velocidade aumentará ou diminuirá de forma constante, a cada segundo. Quando essa velocidade aumenta, dizemos que o seu movimento é acelerado; quando diminui, dizemos que seu movimento é retardado.
O movimento uniformemente variado pode ser descrito por meio de funções horárias, similares àquelas usadas para o movimento uniforme, sendo mais gerais. Além disso, para resolver alguns exercícios relacionados a esse tipo de movimento, é necessário compreender o significado por trás dos gráficos de posição e velocidade. Por isso, vamos estudar as diferentes funções horárias do MUV bem como as suas respectivas representações gráficas.
Primeiramente, trataremos da função horária da velocidade, que também pode ser escrita no formato da fórmula usada para o cálculo da aceleração média, confira:
a - aceleração (m/s)
t - intervalo de tempo (s)
A fórmula mostra que a velocidade de um móvel varia de forma linear com a sua aceleração, ou seja, supondo que um corpo tenha uma aceleração de 3 m/s², a sua velocidade aumentará em 3 m/s, a cada segundo.
Se prestarmos atenção ao formato da função horária da posição, veremos que ela se trata de uma função de primeiro grau do tipo y = a + bx, conhecida como equação da reta. No caso da função horária da velocidade, o coeficiente a, chamado de coeficiente linear, é a velocidade inicial do móvel, enquanto o coeficiente b, conhecido como coeficiente angular, é a aceleração desse móvel.
"No gráfico, vemos duas retas, uma vermelha e uma azul, que representam o movimento de dois móveis. Estes partem do repouso (v0 = 0) e passam a acelerar de forma constante. Um segundo após sua partida, o móvel em azul está com uma velocidade de 4 m/s, enquanto o móvel vermelho está a 2 m/s. Analisando a inclinação das retas, é fácil perceber que a aceleração do móvel azul é maior que a do móvel em vermelho.
"É possível perceber, com base na leitura do gráfico, que a velocidade do móvel em azul aumenta 4 m/s, a cada segundo que se passa, enquanto a velocidade do móvel B aumenta em apenas 2m/s, para o mesmo intervalo de tempo. Desse modo, podemos escrever as funções horárias dos movimentos representados pelas retas azul e vermelha, confira:
S0 - posição inicial
v0 - velocidade inicial
ΔS - deslocamento
Tais equações assemelham-se às funções de segundo grau do tipo ax² + bx + c = 0. Nessas funções horárias de posição e deslocamento, o coeficiente a equivale à a/2 (aceleração dividido por dois), que multiplica o termo t², enquanto a velocidade inicial (v0) representa o coeficiente b.
Com base nisso, vamos mostrar como são os gráficos de movimento uniformemente variado para os casos acelerado, em vermelho, e retardado, em azul, partindo de uma velocidade inicial não nula:
As funções horárias que foram utilizadas para formar os gráficos, representadas pelas curvas vermelha e azul respectivamente, bem como os seus valores de posição, velocidade inicial e aceleração são mostrados a seguir:
A equação de Torricelli é bastante útil quando precisamos resolver algum problema relacionado ao movimento uniformemente variado e não sabemos em qual intervalo de tempo ele ocorreu. Essa equação pode ser facilmente obtida com base nas funções horárias da posição e da velocidade.
Confira como é a fórmula da equação de Torricelli:
"Aceleração escalar média e instantânea
"Aceleração é uma grandeza física vetorial e a sua unidade é o m/s². A aceleração mede a mudança da velocidade em relação ao tempo. Portanto, podemos afirmar que aceleração é a taxa de variação temporal da velocidade de um móvel.
Δv — variação de velocidade
Δt — intervalo de tempo
A aceleração instantânea, por sua vez, é calculada da mesma forma que a aceleração média, entretanto, o intervalo de tempo entre as medidas de velocidade é muito menor. Dizemos que o intervalo de tempo Δt tende a zero. Confira a fórmula que é usada para calcular a aceleração instantânea:
A fórmula de aceleração é bem simples de ser usada: é determinada pela variação de velocidade (Δv) dividida pelo intervalo de tempo (Δt), confira:
Δt — intervalo de tempo
vF — velocidade final
vi — velocidade inicial
Unidade de aceleração
De acordo com o sistema internacional de unidades (S.I.), a unidade de medida de aceleração é o metro por segundo por segundo, ou simplesmente m/s² (que também pode ser escrito como m.s-2). Confira alguns exemplos para compreender melhor a unidade de medida da grandeza aceleração:
Um veículo que se encontrava em repouso e inicia um movimento com aceleração de 2 m/s², terá sua velocidade aumentada em 2 m/s durante cada segundo de seu movimento.
Um móvel que inicia uma frenagem a 3 m/s² terá sua velocidade decrescida em 3 m/s a cada segundo.
Tipos de movimento de acordo com a aceleração
Existem algumas classificações de movimento relacionadas ao módulo da aceleração de um móvel. Confira as mais importantes:
Movimento acelerado: Quando a velocidade de um corpo aumenta a cada segundo, dizemos que o seu movimento é acelerado. A aceleração nesse tipo de movimento é positiva.
Movimento retardado: Nesse tipo de movimento, a velocidade do móvel diminui a cada segundo, por isso dizemos que o seu movimento é retardado. Quando a velocidade do móvel diminui, sua aceleração é negativa.
Movimento uniformemente variado: Quando a aceleração do móvel é constante, dizemos que o seu movimento é uniformemente variado. No caso em que a sua velocidade aumenta de forma constante, o movimento é dito uniformemente acelerado, caso sua velocidade diminua de forma constante, ele é chamado de uniformemente retardado.
Movimento uniforme: O movimento uniforme caracteriza-se por não apresentar aceleração. Nesse tipo de movimento, a velocidade é constante e a aceleração é nula.
"“A mudança de movimento é proporcional à força motora imprimida e é produzida na direção de linha reta na qual aquela força é aplicada.
"Essa lei informa que o módulo da aceleração produzida sobre um corpo é diretamente proporcional ao módulo da força aplicada sobre ele e inversamente proporcional à sua massa. Essa lei é apresentada na equação abaixo:
|a| – módulo da aceleração (m/s²)
|F| - módulo da força (N ou kg.m/s²)
m – massa do corpo (kg)
m – massa do corpo (kg)
a – aceleração (m/s²)
A aceleração produzida sobre um corpo tem a mesma direção e sentido da força resultante sobre ele e é inversamente proporcional à sua massa.
A aceleração produzida sobre um corpo tem a mesma direção e sentido da força resultante sobre ele e é inversamente proporcional à sua massa.
Além disso, o Princípio da Superposição pode ser calculado pela soma vetorial de todas as forças que atuam sobre o corpo:
F – força aplicada sobre um corpo (N)
ΔQ – variação da quantidade de movimento (kg.m/s ou N.s)
Δt – intervalo de tempo (s)
m – massa do corpo (kg)
vF – velocidade final (m/s)
vi – velocidade final (m/s)
“A toda ação há sempre uma reação oposta e de igual intensidade: as ações mútuas de dois corpos um sobre o outro são sempre iguais e dirigidas em sentidos opostos.”
Essa lei permite-nos entender que, para que surja uma força, é necessário que dois corpos interajam, produzindo forças de ação e reação. Além disso, é impossível que um par de ação e reação forme-se no mesmo corpo.
Outra informação contida no enunciado da Terceira Lei de Newton indica que os pares de ação e reação têm a mesma intensidade, mesma direção, porém sentidos opostos. Assim, se produzirmos uma força direcionada para baixo sobre um corpo, receberemos dele uma força de reação direcionada para cima. Por exemplo: se estivermos usando patins e empurrarmos um carrinho de supermercado lotado de compras, seremos empurrados para trás, em decorrência da fraca intensidade da força de atrito entre as rodas dos patins e o piso.
“A toda ação há sempre uma reação oposta e de igual intensidade: as ações mútuas de dois corpos um sobre o outro são sempre iguais e dirigidas em sentidos opostos.”
Essa lei permite-nos entender que, para que surja uma força, é necessário que dois corpos interajam, produzindo forças de ação e reação. Além disso, é impossível que um par de ação e reação forme-se no mesmo corpo.
Outra informação contida no enunciado da Terceira Lei de Newton indica que os pares de ação e reação têm a mesma intensidade, mesma direção, porém sentidos opostos. Assim, se produzirmos uma força direcionada para baixo sobre um corpo, receberemos dele uma força de reação direcionada para cima. Por exemplo: se estivermos usando patins e empurrarmos um carrinho de supermercado lotado de compras, seremos empurrados para trás, em decorrência da fraca intensidade da força de atrito entre as rodas dos patins e o piso.
"Fórmulas das Leis de Newton
As fórmulas utilizadas para definir as três leis de Newton são mostradas abaixo. Confira:
Primeira Lei de Newton
Apesar de ser uma lei qualitativa, podemos esquematizá-la da seguinte forma:
A Segunda Lei de Newton pode ser equacionada a partir da fórmula a seguir:
Terceira Lei de NewtonAs forças de ação e reação em dois corpos distintos apresentam módulos e direções iguais, porém com sentidos opostos. Assim:
Legenda: